FUEL USAGE
(Ranger Hope © 2008, extracts courtesy of A.N.T.A. Publications)

CHECK YOUR PROGRESS NAME:

Speed, distance and fuel consumption:

a. In a vessel that travels at 6 knots consuming 12 litres per hour, how much fuel is required to travel 360 nm before allowing for reserves?

b. In a vessel that travels at 10 knots with twin motors consuming 10 litres per hour each, how much fuel is required to travel 200 nm, allowing for reserves of 20%?

c. How far can a vessel travel with 1000 litres of fuel aboard with a single motor consuming 19 litres an hour to give a constant speed of 20 knots?

d. How far can a vessel travel with 2000 litres of fuel aboard with twin motors consuming 10 litres an hour each to give a constant speed of 10 knots?

e. A vessel has 1000 litres of fuel aboard. Its single motor burns 20 litres an hour at 10 knots. How much extra fuel is required to steam 2000 nm not considering any reserves?

f. A vessel has 480 litres of fuel aboard. Each of its twin motors burn 6 litres an hour when at 11 knots. How much extra fuel is required to steam 600 nm?

Answers:

720 litres.
480 litres
1052.6 nm
1000 nm
3000 litres more
174.5 litres more

Areas of Common Shapes:

Area is the measurement of the footprint for a two dimensional object.

Rectangles - The area of a rectangle is measured by multiplying the Length by the Width.

Example: Find the area of a rectangle measuring 10.2 metres long and 6 metres wide.

AREA = L x W

= 10.2 x 6

= 61.2 mtrs² (square metres)

Exercise:

a. Find the area of a rectangle that has one side 6.2m long and one 4700mm wide.

b. What is the area of a rectangle measuring 870cm long and 3.7m wide.

Answers:

a. 29.14 mtrs²

b. 3.219 mtrs²

Triangles -The area of a triangle is calculated by multiplying half of the base of the triangle by the height of the triangle. Or equivalently, the base can be multiplied by the height and the result then divided by two.

Example: What is the area of a triangle with a base of 3.8m and 1.1m high?

Area (A) = ½ x B x H

A = ½ x 3.8 x 1.1

= 2.09 mtrs² (square metres).

Exercise:

c. Find the area of a triangle with a base of 260cm and a height of 0.85m. Give your answer in square metres correct to 3 decimal places.

d. What is the area of the triangle above? Give your answer in cms²

Answers:

d. 0.21 mtrs²

e. 1200.00 cms²

Trapeziums - A trapezium is a four sided figure that has TWO parallel sides.

The area of a trapezium is calculated by multiplying half its height by the sum of

the two parallel sides.

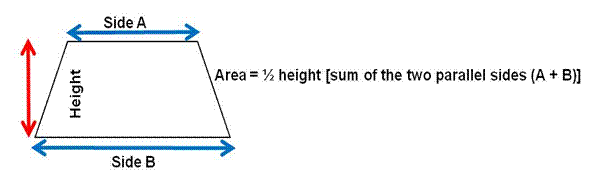
Text Box:

Where A & B are the parallel sides and H is the perpendicular (shortest) distance between them, the height. Note: Do not measure up one of the sides.

Example: What is the area of a trapezium having parallel sides of 2.12m and 3.1m which are 1.2m apart.

Area (A) = ½ x (A + B) x H

A = ½ x (2.12 + 3.1) x 1.2

A = ½ x (5.22) x 1.2

= 3.132mtrs²

Exercise

f. Calculate the area of the trapezium below.

g. Find the area of a trapezium having parallel sides 600mm apart if these sides are 1.23 and 2.32 metres long respectively. Answer in square metres.

Answers

f. 5.56mtrs²

g. 1.065mtrs²

Circles - The area of a circle is given by using the formula:

Text Box:

Where: π = pi = approximately 3.14, or as given by your calculator.

r = radius = half of the diameter of a circle.

Example: Find the area of a circle with a diameter of 2.6cm. Give your answer to 2 decimal places.

Area = π x (½ x 2.6)²

= π x 1.3 ²

= 5.309291585

= 5.31 cms²

Exercise:

h. Find the area of a circle with a diameter of 4.12 metres. Give your answer in square metres, correct to 2 decimal places.

i. Calculate the area of a circle that has a radius of 55cm. Give your answer in square metres correct to 2 decimal places.

Answers:

h. 13.13 mtrs²

i. 0.95 mtrs²

Tank Volumes

(Volume is the capacity measurement for three dimensional objects.)

For the purpose of calculations, the following tanks are defined as “regular” or “irregular” in shape:

Regular shaped tanks:

Irregular shaped tanks:

Tanks that taper also fit into this category.

In practice you may need to make calculations based on an approximate shape. For example, this curved tank can be approximated either to a triangular tank or a quarter of a cylinder depending on the lengths of a and b and the curvature of the side.

Text Box:

Caution - When accurately calculating tank volumes the internal measurements of the tank (excluding the thickness of the tank walls) should be used. If given the external measurements of a rectangular tank, you must subtract the material thickness from both ends of the tank.

Length - 2 x the material thickness

Width - 2 x the material thickness

Depth - 2 x the material thickness

This calculation is complex with irregular shape tanks so workbook omits material thickness in examples, but in practice allowances must be.

Rectangular Tanks:

To calculate the volume (and capacity) of rectangular tanks the formula is Length multiplied by the Width multiplied by the Height of the tank.

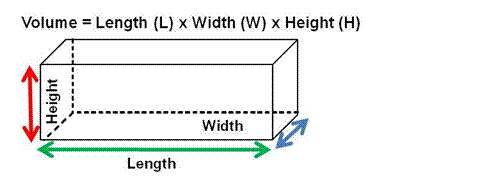
Text Box:

Example: If a tank is 3.1m long and 2.24m wide, what would be its volume if the depth of the tank is 1.1m.

Volume (V) = L x W x H

= 3.1 x 2.24 x 1.1

= 7.6384 mtr³

= 7.64 mtr³(in cubic metres to 2 decimal places)

Cylindrical Tanks:

The volume of a cylindrical tank is measured by multiplying the area of the circle by the height or length of the tank.

Example: A cylinder has a circular base of 1.8m in diameter and stands 2.2m high. What is the capacity of the cylinder?

Volume = π r² x h

V = π x 0.9² x 2.2

= 5.595 mtr³

Trapezoidal tanks:

Given the shape of some vessels and the limited space available below decks, it is often necessary to make fuel tanks in an irregular shape.

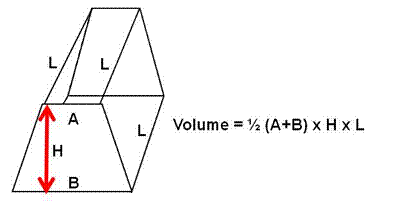
Text Box:

The area of a trapezium is calculated by multiplying half its height H by the sum of the two parallel sides A and B.

Area = ½(A+B) x H x L

Once you have calculated the area of the side ends, you can calculate the volume of the tank by multiplying it by the length L.

Example: Referring to the above shape, calculate the volume if the dimensions of the tank are:

A = 1.5 B = 3 H = 2 L = 4

Area = ½ (A+B) x H x L

= ½ x (1.5 + 3) x 2 x 4

= 4.5 x 4

=18 mtr³or the tank has a volume of 18 cubic metres

Check your progress

a. What is the volume of a tank measuring 7.1m long, 3m wide and 4500mm deep? Give you answer in cubic metres.

b. What is the volume of a ballast tank measuring 3080mm long, 1420mm wide and 64cm deep? Give your answer in mtr³. What is this tank’s capacity in litres, to 2 decimal places.

Remember that 1 Litre = 0.001 mtr³ or 1000 Litres = 1 mtr³

c. What is the capacity of a cylindrical fresh water tank if it has a diameter of 6.2m and a length of 424.2cm? Give your answer to 2 decimal places.

d. What volume of fuel is in a cylindrical tank of 1.2 metres diameter and a height of 3 metres when it is half full?

e. What weight of fuel is in a cylindrical tank of 3 metres diameter and a height of 2 metres when there is an ullage taken of 400mm? Use a specific gravity for fuel of 0.8.

f. What weight of fuel is in a trapezoid tank of 2 metres bottom width and 2.4 metres top width, a height of 1.6 metre and a length of 4 metres? Use a specific gravity for fuel of 0.8.

g. What weight of fuel is used by a vessel travelling 300nm that maintains 10 knots with her single 200 kW engine consuming 125cc per kW per hour? Use SG 0.8.

h. Allowing in the above case for a 25% reserve, what weight of additional fuel would be prudent to load?

Answers:

a. 95.85 mtr³

b. 2.799 mtr³ 2799 litres

c. 12.80 mtr³ 12800 litres

d. 1.69 mtr³ 1690 litres

e. 11.3 mtr³ 11304 litres x 0.8 = 9043.2 kilos = 9.043 tonnes

f. 14.8 mtr³ 14800 litres x 0.8 = 11264 kilos = 11.264 tonnes

g. 750 litres x 0.8 = 600 kilos = 0.6 tonnes

h. An additional 150 kilos = 0.15 tonnes