VESSEL POSITIONING TECHNIQUES (PLOTTING)
(Extracts courtesy of A.N.T.A. publications,
Ranger Hope © 2008 www.splashmaritime.com.au)
Cross Bearings
Ranges of Two or More Points
Combined Range and Bearing
Bearing and Sounding
Line of Soundings
Running Fix
Doubling Angle on the Bow
Four Point Bearing
Transit Bearing
Danger or Clearing Bearings
Vertical Sextant Angle
Positions
Course
Conventions, Symbols
Speed, Distance and Time
Tidal Streams and Current
Plotting Positions
Dead Reckoning or Estimated Position
Leeway
Counteract Tide, Current or Wind
Running Fix with Tide
Plotting a Position
When latitude and longitude are given, or read from a GPS receiver, the preferred
method of plotting the position is to first identify the approximate area and
use the parallel rules to lay off the given parallel of latitude from the closest
side latitude scale. Longitude can then be measured along this parallel using
dividers set against the appropriate longitude scale.
To plot a position given bearing and distance from a known point, parallel rules
are used to mark off the true bearing by “walking” them from the
nearest compass rose.
Dividers or compasses are then used to mark off the distance from the point.
Remember that distance is measured from the adjacent latitude scale.
By
Cross Bearings
Bearings taken may be:
a) Relative - as with pelorus or radar in ship’s head up display.
b) Compass - using the magnetic compass
c) Gyro - when a gyro repeater is used.
In any case the bearing must be converted to true before laying it off on the
chart.
Each position line (LOP) should be identified by a single arrow at the end of
the line away from the object observed.
When position lines intercept at (or nearly at) a point, that point should be
encircled and the time of the fix noted alongside.
When position lines fail to intercept at a point and a “cocked hat”
results, it may be due to any of the following:
a) Too long a delay between taking bearings
b) Wrong identification of an object
c) Error in plotting
d) Compass error wrongly applied
e) Unknown compass error
f) Poor survey of the area
If the cocked hat cannot be reduced or eliminated by any of the above checks then the position of the ship should be taken as that part of the cocked hat which will place the ship in most danger.
Figure
1: Fix by cross bearings showing a “cocked hat”
By
Ranges of Two or More Points
This is the preferred method when fixing the position by radar observations.
Ranges taken from the radar are generally more accurate than radar bearings.
Avoiding the steps necessary to convert relative or compass bearings to true
also reduces the chance of error.
Ranges must be taken off the adjacent latitude scale and the relevant arc plotted
on the chart using compasses. Both ends of the arcs should be marked with a
single arrow, the point of intersection circled, and the time of the fix written
alongside.
Selection of objects for ranges is as important as it is with bearings, and
any cocked hat should be treated in much the same way.

Figure 2: Fix Using Radar Ranges
By Combined Range and Bearing
When only one suitable object is available the position may be fixed with a
single bearing of that object combined with its range. Although the range would
usually be measured by radar it is still preferable to obtain the bearing visually.
The bearing can usually be taken more accurately by visual means.
By
a Bearing and Sounding
This method may be used providing :
· Allowance is made to reduce the sounding to chart datum.
· The depth contours are well defined.
· The contour in question only crosses the position line in one possible
place.
· The depth contour crosses the position line at a wide angle.
Figure 3: Fixes Using Soundings
By a Line of Soundings
By taking soundings at a regular time intervals and converting that time to
distance run, a line of soundings may be constructed along the edge of a piece
of paper. If this is manoeuvred across the chart parallel to the vessel’s
track a match may be found with charted soundings. This again required converting
to chart datum and a chart with sufficient soundings. Even then there may be
more than one track where a good match can be found. Any position obtained by
this method should therefore be treated with a great deal of caution and checked
by other means as soon as possible.
By
Running Fix
Transferring a position line was mentioned earlier as a means of reducing a
cocked hat when there is an unplanned delay between bearings. It is more commonly
used when only one object is available for bearings and there is no means of
measuring the range. In this case there is a planned delay between bearings
so that the change in bearing will provide an acceptable angle of cut.

Figure 4: A Running Fix
The first position line is transferred forward by the distance and in the direction
the vessel is thought to have travelled between bearings. The transferred position
line is drawn parallel to the first position line. It is marked with double
arrows at each end. The Fix is where it intersects the second position line.
Example:
A vessel is steering 312°(T) at 10 knots. At 1400 Lady Musgrave Island is
observed bearing 280°(T). At 1442 it bears 252°(T). Assuming there is
no set or drift between bearings, find the position at 1442.
Doubling
the Angle on the Bow
This is a refinement of the running fix which takes advantage of the properties
of isosceles triangles.
As illustrated the angle on the bow when the first bearing is taken is 35°.
The time of this bearing is noted and the bearing then carefully watched until
the angle on the bow doubles to 70°. The triangle formed by the two position
lines and the course line is isosceles, therefore the range at the time of the
second bearing is equal to the distance run between bearings.

Figure 5: Doubling the angle of the bow
In practice the distance run is simply calculated (speed x time) and this distance
used as a range in conjunction with the second bearing.
Example:
A ship steering 058°(T) observes a single light at 0606 which bears 035°
relative. At 0636 the light bears 070° relative. Ship’s speed 10 knots.
What is the true bearing and distance of the light at 0636?
Time between bearings = 30 minutes (0.5 hrs)
So distance run = 10 x 0.5 miles
= 5.0 n. miles
True course = 058°(T)
Relative bearing = 070°(R)
So true bearing = 128°(T)
Answer: At 0636 the light bears 128°(T) at distance 5.0 n.miles.
The
Four-Point Bearing
This is a further refinement of the running fix in which the first bearing is
taken when the object is at four points (45°) on the bow. When the object
is on the beam the range will be the same as the distance run since the first
bearing was taken. The disadvantage of the four point bearing is that the range
of the single object is not known until it is abeam. This is of little help
in passing at a safe distance.
The four point bearing is illustrated below:

Figure 6: Four Point Bearing
With all types of running fix the accuracy of the final position depends on
the accuracy of the prediction of the course and distance made good between
bearings.
The
Transit Bearing
When two charted objects come into line they are said to be in transit. It has
already been shown how a transit can be used to check the compass error. A transit
can also be used to obtain a fix in conjunction with another position line such
as a range (or be used to obtain a fix in conjunction with another position
line such as a range (or even a sounding) without use of the compass. Both possibilities
are illustrated below.

Figure 7: Transit with Radar Range
Figure 8: Transit with Sounding
Danger or Clearing Bearings
Many ports have provided leading lights or shapes to guide mariners safely into
harbour, avoiding shoals and other dangers.
In places where such aids are not provided, the navigator may still be able
to select a leading line provided by the transit of natural features. Thus approaching
an anchorage with a coastal hill in transit with a more distant peak may ensure
that the vessel clears dangerous rocks.
The advantage of a transit is that the mariner is assured of a safe approach
regardless of any compass error.
When a suitable transit is not available a single danger bearing may be taken from the chart. As shown below - so long as land’s end is bearing 244°(T) or less then the danger will be avoided.

Figure 9: Single Danger Line
A single position line may also be transferred ahead to give a course to steer
to safely clear a charted danger. As illustrated below the vessel can safely
turn on to a course of 312°(T) at 0430 hrs. and be assured of clearing the
danger so long as the speed is accurately known and allowance is made for any
set and drift.

Figure 10: Transferred Clearing Bearing
Vertical Sextant Angle
The distance off a light can be found by taking the vertical angle the light
subtends at the vessel above sea level (See Figure 11).
Figure 11: Vertical Sextant Angle
The height LS can be found on the chart. The angle at V can be measured with
a sextant. Using nautical tables, enter the section called ‘distance by
vertical angle’ which gives the distance off using the sextant angle and
height of the object in feet or metres.
Example:
Assuming the vertical angle at V to be 40° of arc and the height of the
light SL to be 85 metre (280 ft.) the distance off (SV) would be 3.9 metre.
Set your compasses to 3.9 metre and scribe an arc with the lighthouse as centre.
If a bearing is taken at the same time a fix can be obtained from only one object.
Figure 12
When using the sextant, set it at 0° and the view through the telescope
would be as in Figure 13.
Figure 13: Sextant Image
The image of the lighthouse is brought down to sea level as in Figure 14.
The reading on the sextant, corrected for any index error is the Vertical Sextant
Angle.
Figure 14: Sextant Image
Explanation of Instruments
If the error is “OFF” the Arc add to Sextant Reading.
If the error is “ON” the Arc subtract from Sextant Reading.
Selection of suitable points for bearings and radar ranges.
When selecting objects or features for observation of their bearing or range,
the following should be taken into consideration
· The objects must be conspicuous
· They must be charted
· There must be no danger of ambiguity
· Ends of land should be steep to avoid errors due to tide level and
possible lines of breakers
· When two objects are chosen the angle of cut should be as near 90°
as possible.
· When three objects are selected the angle of cut should be as near
60° as possible.
· Close objects are preferred to distant objects because any error will
be exaggerated by long position lines.
Plotting with Current
Positions
Course
Conventions, Symbols
Speed, Distance and Time
Tidal Streams and Current
Plotting Positions
Dead Reckoning or Estimated Position Leeway
Counteract Tidal Stream or Current
and Wind
Running Fix with Tide
Plotting with Current
Positions
FIX + time (Fix) This is the position of a vessel as determined by the intersection
of two or more position lines.
It is denoted by the symbol below with the time of observation.
D.R. + time (Dead Reckoning)
This is the position based on the true course and distance run through the water
from the last known position. Denoted by the symbol below with time
E.P. + time (Estimated Position)
This is the position of best possible approximation based on course and distance
since the last known position, with an estimation for Set, Drift and Leeway.
Denoted by the symbol, with time.
COURSE (Co)
The Intended Heading
Course to Steer. The course related to the compass used by the helmsman.
Course made good. The (CMG) is the actual course over the ground between 2 observed
positions.
Distance and Speed These are generally related to the vessels movement through
the water. i.e. ascertained from the log or calculated from engine revs.
Distance
made good These are related to the
Speed made good. measurement between 2 observed positions i.e. over the ground.
SET The direction towards which a current and/or tidal stream flows.
DRIFT The distance covered in a given time due to the movement of a current
and/or tidal stream.
RATE OF DRIFT The speed of the current and/or tidal stream.
DRIFT ANGLE The angular difference between the track through the water and the
track over the ground.
LEEWAY The effect of the wind blowing the vessel to leeward. It depends on the
winds strength and direction, type of vessel and its draught. Generally estimated
from experience.
LEEWAY ANGLE The angular difference between the ships heading and the track
through the water.
POSITION LINE It is a line on the chart on which the vessel lies or has lain.
It may be straight as in a bearing or curved as in ranges.
Conventions, Symbols, Abbreviations - On the chart we use the following conventions.
These symbols are used in the examples in this book.
Speed,
Distance and Time
Many problems in navigation require an ability to manipulate these three associated
values. Having measured a distance along an intended track it may be necessary
to work out an estimated time of arrival at a given speed; or to calculate the
speed required to arrive at a destination at a certain time (to catch the tide
for example). It may also be necessary to calculate the distance travelled in
a certain time so that the dead reckoning or estimated position can be plotted
(see Outcome 6).
The three equations which may be needed are:
DISTANCE = SPEED X TIME
SPEED = DISTANCE/TIME
TIME = DISTANCE/SPEED
Tidal
Streams and Current
Tides are the periodic rise and fall of the level on the sea due to various
celestial bodies.
The ‘tidal stream’ is the horizontal movement of water that result
from the tides.
In general the direction of flow will change once or twice a day depending on
the type of tide.
A ‘current’ is the horizontal movement of water not caused by tides
and generally follows some seasonal pattern.
Example: The East Coast current of Australia. Winds tend to influence the rate
of currents.
Interpreting information on ‘currents’.
Consulting the symbol book 5011 you will find the symbol for current is:

Figure. 15: “Current” Symbol on a Chart
It may have an average rate above the line as shown.
Have a look at the smaller scale charts to see if you can observe the symbol
and its direction. You may also find reference to currents under the title in
the holes.
![]()
Figure. 16: “Current” Information on a Chart
If you consult the Australian Pilot Vol 111, surface currents are given on a
quarterly basis, as in the diagram for January shown on the following page in
figure 17.
The surface currents covered by this volume are described in some detail from
pages 16-18 and also in the more specific area text.

Figure 18: January Surface Currents from Australian Pilot Vol 111
We will now consider the interpretation of information on ‘tidal streams’.
These are mentioned in Australian Pilots, covering the area for each volume.
For example ‘tidal’ streams are found on pages 18 and 19 of Volume.
III of this publication.
An example from the specific text is shown below for Stonehaven Anchorage in
Figure19.

Figure.
19: Tidal Streams Stonehaven Anchorage
Extract from Australian Pilot Vol. 111
On the chart the symbols for tidal streams are shown below - in figure 20 make
sure you know the difference between ebb and flood tidal stream. The rates are
generally shown on the arrow.
Figure 20: “Tidal Stream” Chart Symbols See Appendix Chart 5011 – Symbols.
On certain charts you may notice tables as shown in Figure 21.
They contain position for which tabulated tidal stream data are given.

An example of a chart area is given in Figure 21, Shoal Water Bay.
The hours before and after high water relate to a standard port, which can be
found from the Australian National Tide Tables etc.
The direction is given for each hour and the rate for Spring and Neap tides
is given in knots.
Note how the tidal diamonds relate to the chart area. They are coloured Magenta on all charts.
The diamond
with an ‘F’ in it is close east of the word ‘North’
in North Channel.
Figure 21: Extract from Chart AUS822 showing tabulated Tidal Stream Data for Positions in Shoalwater Bay
Another type of tidal stream information is produced in the Australian National
Tide Tables, and is given in graphical form. They cover 3 port areas.
A. Darwin
B. Broome
C. Sydney Harbour
They are to some extent self explanatory. The diagram for Broome is shown in
Figure 22.
Notice how the stream changes well before high water, and for practical purposes around the time of low water.

Figure 22: Tidal Stream Diagram - Broome
In the Torres Strait specific stream data is given for each day at Hammond Rock. Read the notes in Appendix B from the tide tables about this area.

Figure 23: Hammond Rock - Tidal Stream Data (From Australian National Tide Tables)
Plotting Positions
Plotting a Dead Reckoning (DR) and Estimated Position’s (EP’s)
It is now time to consider plotting DR’s and EP’s - finding Set
and Drift and making allowance for tides, currents and wind. As you will remember,
a D.R. position uses true course steered and vessels speed only. If we start
at position P (fix) and steer 090°T for one hour, we arrive at position
Q (D.R.) as shown on the chart extract drawing Figure 24.
If the navigator is aware of the existence of a current or tidal stream he can
make an allowance for it and plot an Estimated Position (E.P.)
As illustrated etc. (see below)
Fig 24 Plotting a D.R. and E.P.
As illustrated the vessel has been steering 090°(T) for one hour at 7.0
knots. The navigator estimates that the tide has been running to the north at
2 knots during that time. Given the starting position at “P” the
D.R. is plotted at “Q” - then one hour’s set and drift is
applied to give the estimated position at “R”
Leeway
We will now consider Leeway.
If a vessel is steering 090°(T) with a southerly wind, which is expected
to cause 10° leeway (this is ascertained through vessel experience) then
the vessel’s track will be 100°(T).
In practice it would be far more sensible to adjust the vessel’s course,
counteracting expected leeway so that the desired track is achieved. See example
Fig 26.
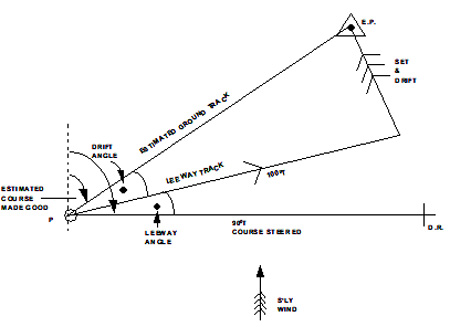
Figure 25: Estimating Track after allowing for Set, Drift and Leeway
Example:
A vessel is required to make good a course of 060°(T) in a strong South
Easterly wind which is expected to cause 5 degrees leeway.

Figure 26: Allowance for Leeway
Course to make good 060°(T)
To counter leeway + 5
Course to steer 065°(T)
Finding
Set and Drift
If a reliable fix places a vessel in a position which is different from the
D.R. position, that difference will be the result of current and/or tide (and
possibly wind).
In the illustration below a vessel obtained a good fix at 0600 (position “A”)
and set course 285°(T) at a speed of 10 knots. At 0630 the D.R. was at position
“B”, but a reliable fix showed the true position to be at “C”.
In this case the set is 050°(T) and the drift is 1.0 mile. Since the time
period was thirty minutes the rate of the current was 2 knots.

Figure 27: Finding Set and Drift
To
Counteract a Known Tidal Stream or Current
If the navigator knows the direction and speed of a tidal stream, the course
to steer to counteract that tidal stream can be found.
From the starting point “A”, a vessel needs to make good a track
of 080 (T) to arrive at position “B”. The tide is known to set 200
(T) at 2 knots. The vessel’s speed is 10 knots.
To find the course to steer:
1. Lay of the required course to make good, “AB”.
2. Plot one hour’s set and drift from “A” to “C”.
3. With centre “C” lay off ship’s speed - the distance she
will travel through the water in one hour - to point “D”
4. The direction “CD” is the true course to steer from “A”
5. The distance “AD” is the speed that will be made good
6. To find the E.T.A. at “B” the distance “AB” is divided
by the speed made good “AD”.

Figure 28: Counteracting a known tidal stream or current
To
Counteract Tidal Stream and Wind
The tidal stream must be counteracted first. The correction for leeway is applied
to the result.

Figure 29: Constructing a Triangle from Tidal Stream and Wind
The Triangle A.C.D. is for construction only and can be of any size depending
on chart scale.
For ease of calculation it is usually made to 1 hr. or intervals thereof.
Example:
It is required to make good a course of 090°(T) with a tide setting 220°(T)
at 4 knots and a northerly wind causing an estimated leeway of 6 degrees. Ship’s
speed is 13 knots. What is the true course to steer?

Figure 30: Counteracting Tidal Stream and Wind
From the vector plot - course to steer to counteract tide 076°T
to counteract wind -6°
Therefore: course to steer to counteract wind and tide 070°T
Running
Fix with Tide
As was previously discussed, the accuracy of a running fix depends on the accuracy
of the course and speed made good between bearings.
If the navigator is aware of the existence of a tidal stream or current, allowance
must be made for set and drift experienced in the time interval between bearings.
If the vessel is steering 040°(T) at 10 knots, the tide is setting 090°
at 3 knots and the run is 30 minutes between bearings then the first bearing
must be transferred ahead 5 miles in a direction of 040° and 1.5 miles in
a direction of 090°. This is illustrated below.

Figure 31: Running Fix and Tide