TIDES AND THEIR CALCULATION
(Material contains extracts intended for study and research only-Courtesy of ANTA Publications and the AHO Ranger Hope © 2016)
Calculations involving Standard and Secondary Port
The use of High and Low Water to determine Keel Clearance
The factors which cause tides
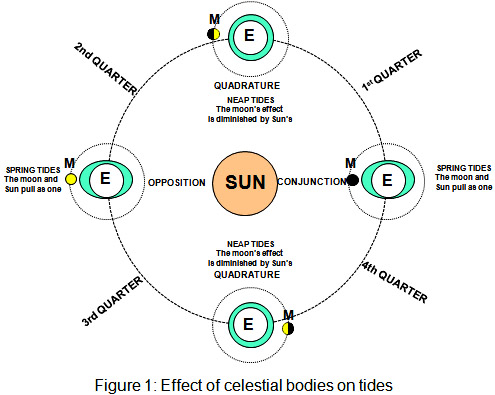
Tides are caused by the attractive forces of the sun and moon. Due to its closeness to the earth the effect of the moon is far greater than that of the sun. Therefore the moon largely controls the time of high and low waters. The relative position of the sun and moon will determine whether the sun’s force increases the moon’s effect on the tide or decreases its effect.
When the sun and the moon are working together to distort the envelope of water surrounding the earth, they are either in opposition or conjunction and spring tides are the result. When the effects are opposing each other the sun and moon are said to be in quadrature and neap tides result. Opposition occurs with a full moon and conjunction with a new moon as shown in Figure 1.
The shape of the envelope of water is highly exaggerated in the diagram. In reality the rise and fall of tides in the middle of the oceans is barely noticed. It is only when the movement builds up approaching a coastline that the effect is significant. It can therefore be seen that the shape of the coastline will also have considerable effect on tidal patterns and heights. Shallow funnelling estuaries with low change in depth gradients may develop higher tidal ranges, and areas behind obstructing islands may experience double tides for each side.
Strong onshore winds will tend to hold the tide up, and abnormally low atmospheric pressure will further increase the height of the tide. When both of these meteorological effects occur together, as they may do with a tropical cyclone, the effects from storm surge and flooding can be devastating.
Tides and Chart datum
Due to the complexity of the cause of tides, tidal predictions are based on the most frequent set of conditions. They are related to a standard level called Chart Datum. Chart Datum is selected at a level below which the tide will seldom fall. Older Australian Charts used the chart datum of the mean of the lower low water springs (MLLWS). Since there were still a considerable number of occasions when tidal heights fell below this level, charts are now produced with the datum of Lowest Astronomical Tide (LAT), being the lowest the tide that can be predicted due to the effects of celestial bodies’ gravitational attraction under average meteorological conditions.
Soundings on charts are given below Chart Datum. Drying heights of rocks and banks are given above Chart Datum. Heights of land and land based structures on charts are expressed as above Mean High Water Springs.
The heights of High and Low water on tide tables are the heights of water above the chart datum.

Range of Tide is the difference in height between Low and High Water.
The Duration of Tide is the time interval between successive High Waters.
The Duration of Rise (flow) is the time interval from Low Water to High Water.
The Duration of Fall (ebb) is the time interval from High Water to Low Water.

In most cases standard tides flow in/out in just over six hours. The flow rate approximates a sine curve, being initially minimal, then greatest at half tide then diminishing again at the top/bottom of the tide. An estimate of tide height at a time is possible using the “rule of twelfths”. In this method the tidal range is divided by twelve and it is assumed that the 1/12 of the range flows in the first hour, another 2/12 in the second hour, another 3/12 in the third hour, and so on. The twelfths are summed to estimate the volume that has flowed at any selected time.
Basic tide tables
Many versions of tide tables are available in print and on the internet. Below are detailed the extraction of times and heights of high and low water for a Standard Port from a NSW Maritime (RMS) tide chart for Friday 28th December 2012.

Figure 4.-Basic tide tables
Example:
Find the time and height of low water at Clyde Bridge on Friday 28th December 2012.

Figure 5.-Extracting data from basic tide tables
The HW at Sydney listed is 18:00 (UTC) + 00:15 later at the bridge = 18:15 (UTC).
Note that the times stated are Zone time (UTC). In NSW summertime daylight saving is in force between October and April so a local time is correction by adding one hour is necessary in December.
Therefore high water local (daylight saving) time of is 18:15 (UTC) + 1 hour = 19:15.
The yellow ball indicates that it is the time of the full moon in conjunction when spring tides are reaching their maximum. It is the reason that 1.73 metres of tide flow in over the chart’s soundings on the Friday. More information is found at
http://www.bom.gov.au/oceanography/projects/ntc/tide_tables.shtml
Intertidal heights and times
The tide height at a time will often be needed to ensure safe entry over a shoal patch or to anticipate how much rode is required to anchor. The simplest (and least accurate) way of estimating this is to make an assumption that the height and duration of tidal flow follows a sine curve. Clearly it will be wise not to rely on the estimates calculated, and to allow additional clearance for the vessel as circumstances require. The methods available are the Rule of Twelfths (described earlier) and the Tidal Graph (AH130).
Example 2.– Rule of Twelfths:
Find the time and height of 1.0 mtrs over LAT at Sydney on 28th December 2012.

Figure 6.-Times and heights of HW and LW
Over the six hours duration the tide will fall on the first hour, then 2/12, then 3/12, then 3/12, then, 2/12 and finally on the last hour before low tide, 1/12:
The range of tide is 1.73m – 0.36 m = 1.37 m.
1/12 of the range is 1.37m ÷ 12 = 0.114m.
Therefore the tide will have fallen to 1.0m at:
1.00 ÷ 0.114m = 8.77 twelfths (approximately 1/12 + 2/12 + 3/12 + 3/12) and just before the fourth hour of the ebb.
0800 + almost 4 hours = at just before 1200. When daylight saving correction is added the time of 1.0m over LAT is estimated at just before 1300 (say 1245).
Example 3.–Use of tidal graph: (Link here to a blank Tidal Graph)
Find the time and height of 1.0m over LAT at Sydney on 28th December 2012.

Figure 7.-Tidal graph AH130
The tidal graph includes instructions for it use to find any intertidal time and height When daylight saving correction is added the time of 1.0m over LAT is estimated at just before 1130 + 1 hour = 1230.
Note - this calculation assumes the sine curve ideal of tidal flow, unlikely to be matched in reality so additional clearance should be allowed for.
Mariners that ply in more distant or remote areas will require the Admiralty Tide Table (worldwide) or the Australian National Tide Tables (Australian region). In order to provide tidal information for the hundreds of ports the ANTT provide detailed daily predictions for Standard (large) ports and tables to calculate the difference at a Secondary (smaller) port. The Standard Port acts as a reference station where predictions are based on continuous observation and contain changes in conditions due to meteorological conditions.
The information given in the ANNT for each standard port is the predicted times and heights of high and low water. Secondary Ports or Subordinate stations are based as near as practicable on Standard Port tidal characteristics in the area. The predictions for tidal times and heights for secondary ports are made by the application of time and height differences to the standard port.

More information is found at http://www.hydro.gov.au/prodserv/publications/antt.htm
Calculations involving a Standard and Secondary Port
While all tides are composed of both diurnal (once a day) and semi-diurnal (twice a day) components, the ANTT lists in Table 1-Tidal Levels of Standard Ports as either Part 1 - Predominantly diurnal tides or Part 2 - Predominantly semi-diurnal tides
Diurnal tides - A diurnal tide has one high water (tide) and one low water (tide) per day. Typically with a diurnal tide each successive high or low tide is 24 hours and 50 minutes apart, this is the length of one lunar day.
Semi-diurnal tides - A semi-diurnal tide occurs when there are two high waters (tides) and two low waters (tides) per day. Typically the time between each successive high or low tide is 12 hours 25 minutes, this is half of one lunar day.
When using the ANTT Standard and Secondary Port calculation forms it will be noted that there are two versions. The version for Table 1-part 1-Predominently Diurnal Tides is entered with MHHW and MLLW, whereas version for Table 1-part 2-Predominently Semi-diurnal Tides is entered with MHWS and MLWS.
For calculations you will need to access the calculation forms and the ANTT:
(Link to Standard/secondary Calculation forms -Part 1 diurnal and Part 2 semi-diurnal)
(Link to Australian National Tide Tables extracts 1998)
Example 4.–Diurnal ports:
You require the times and heights of high and low water at Port Campbell for the 1st February 1998, using the ANTT 1998:
First look up Port Campbell in the Port Index and find its number is 61360.
Next look for 61360 in Part 3-Secondary Ports and find its Standard Port is Portland.

Figure 9.-Extract from ANTT Part 3-Secondary Ports
Next look for Portland in Part 1-Tidal predictions for Secondary Ports and find the times and heights of tides on 1st February 1998.

Figure 10.-Extract from ANTT Part 1-Standard Ports
Next check if it is a Diurnal or semidiurnal listed port in Table 1-part 1 or 2

Figure 11.-Extract from ANTT Table 1-Part 1-predominantly diurnal ports
Instructions to complete Diurnal calculation form:
Now you can extract the above information from the ANTT to enter the Diurnal calculation form (MHHW and MLLW version).
From Part 1 enter time and heights of HW/LW Portland on 1st Feb. (Box 1 & 2)
From Part 3 find MSL (Box MSL) & MHHW and MLLW (Box 4). Subtract (Box 5)
From Table 1-part 1 find LAT correction for (Box 6), reverse its tabulated sign from + or -, then arithmetically sum in (Box 7).
Now subtract the MSL from heights in (Box 7) and enter results in Box 8 (Note, HW are normally positive, LW are negative).This completes Standard port data.
From Part 3 (Port Campbell No. 61360) extract the mean time difference in (Box 9), the MSL (Box 10), and MHHW, MLLW (Box 11)
Box 12 is entered with the difference between MHHW and MLLW
Box 13 Range Ratio is found by (Box 12) ÷ (Box 5)
0.9 ÷ 0.8 = 1.125
Box 14 multiply the heights in (Box 8) by (Box 13)
+0.40 x 1.125 = +0.45
+0.10 x 1.125 = +0.11
-0.20 x 1.125 = -0.22
-0.30 x 1.125 = -0.34
Box 15 corrects the few secondary ports not referenced to LAT (In Part 4 ANTT)
Add the mean time difference (Box 9) to times in Box 1 and enter in Box 16.
Add the values of (Box 10) to (Box 14) to (Box 15)

Figure 12.- Diurnal calculation form
Example 5.–Semi-diurnal ports:
You require the times and heights of high and low water at Ettalong for the 16th June 1998, using the ANTT 1998.
First look up Ettalong in the Port Index and find its number is 60325.
Next look for 60325 in Part 3-Secondary Ports and find its Standard Port is Sydney.

Figure 13.-Extract from ANTT Part 3-Secondary Ports
Next look for Sydney in Part 1-Tidal predictions for Secondary Ports and find the times and heights of tides on 16th June 1998.

Figure 14.-Extract from ANTT Part 1-Standard Ports
Next check if it is a Diurnal or semidiurnal listed port in Table 1-part 1 or 2

Figure 15.-Extract from ANTT Table 1-Part 1-predominantly diurnal ports
Instructions to complete Semi-diurnal calculation form:
Now you can extract the above information from the ANTT to enter the Semi-diurnal calculation form (MHWS and MLWS version).
From Part 1 enter time and heights of HW/LW Sydney on 16th June. (Box 1 & 2)
From Part 3 find MSL (Box MSL) also the MHWS and MLWS (Box 4). Subtract MHWS from MLWS in (Box 5)
From Table 1-part 1 find LAT correction for (Box 6), reverse its sign from + or -, then arithmetically sum in (Box 7). The example given has a LAT correction of 0.
Now subtract the MSL from heights in (Box 7) and enter results in Box 8 (Note, HW are normally positive, LW are negative) to complete the Standard port data.
From Part 3 (Ettalong No. 60325) extract the mean time difference in (Box 9), the MSL (Box 10), and MHWS, MLWS (Box 11)
Box 12 is entered with the difference between MHWS and MLWS
Box 13 Range Ratio is found by (Box 12) ÷ (Box 5)
0.8 ÷ 1.2 = 0.66
Box 14 multiply the heights in (Box 8) by (Box 13)
+0.8 x 0.66 = +0.53
+0.5 x 0.66 = +0.33
-0.5 x 0.66 = -0.33
-0.4 x 0.66 = -0.26
Box 15 corrects the few secondary ports not referenced to LAT (In Part 4 ANTT)
Add the mean time difference (Box 9) to times in Box 1 and enter in Box 16.
Add the values of (Box 10) to (Box 14) to (Box 15)

Figure 16.- Semi-diurnal calculation form
The use of High and Low Water to determine Keel Clearance
First you are required to know your deepest draft. This is usually at the stern of the vessel.

Next find from the chart the soundings/drying heights. Remember these are below and above chart datum respectively.

The datum for tides needs to be the same as the datum for soundings. In Australia the practice is to establish datum at the Lowest Astronomical Tide (L.A.T.).
Next find the heights of high and low water for the area.

The formula is:
Under keel = (Height of tide + Sounding) - (Vessel’s Draught)
Remember that a drying height is a negative (-) sounding.

Example 6:
Consider a place in Sydney when the height of HW is 2.8m. The vessel’s draught is 1.5 mtr. What is the under keel clearance over a rock of drying height 0.9 mtr?

Under keel clearance = (Height of tide + Sounding) - (Draught)
(Drying height of 0.9 mtr as a negative sounding)
= (2.8 - 0.9) - (1.5)
= 1.9 - 1.5
= 0.4m
Under keel clearance = 0.4 metres at High Water